Atcoder ABC 284 D – Happy New Year 2023 解法 | monkeyエンジニアブログ

この記事では Atcoder の解答方法について説明していきます。

私ですが数学の知識は高校レベルくらい（それもかなり忘れてしまった）で、Atcoder の解説ページの洗練された説明では？？？のオンパレード。

なのでいつも自分の中で数学的な言葉を使わないように噛み砕いて理解しようと努力しています。

でも実際に私のような方も多くいるのでは？と思い本記事を作成しました。

Atcoder の解説を読んでもよくわからない…となった方にとって、一助になれば幸いです。

問題
パッと思いつくこと
解法に至るまで
まとめ

問題

D - Happy New Year 2023

AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.

パッと思いつくこと

N を素数の組み合わせ（p, q）で表せる数を求めるのですから、素因数分解してその中から $p^{2}q$で表せるような数値の組み合わせを探せば良さそうだな…というのはパッと思い付きます。

素因数分解を行うアルゴリズムとしては試し割りというものがあります。これは単純に N までの数値を 2 から $\sqrt{n}$ まで単純に割っていくというものです。計算量は $O(\sqrt{n})$ です。

int main() {
  int n;

  cin >> n;

  vector<pair<int, int>> res;

  for (int i = 2; i * i <= n; ++i) {
    if (n % i != 0) {
      continue;
    }

    int x = 0;

    while (n % i == 0) {
      ++x;
      n /= i;
    }

    res.push_back({i, x});
  }

  if (n != 1) {
    res.push_back({n, 1});
  }

  for (int i = 0; i < res.size(); ++i) {
    if (i != res.size() - 1) {
      cout << res[i].first << "^" << res[i].second << " * ";
    } else {
      cout << res[i].first << "^" << res[i].second << endl;
    }
  }

  return 0;
}

しかし、本設問では $N \leq 9 \times 10^{18}$ という条件があります。なのでこの計算量は $O(10^{9})$ となり、TLE になってしまいます。（3 sec の実行時間ではせいぜい $O(10^{7})$ くらいが限界です。）

なので別の方法を考えていく必要がありそうです。

解法に至るまで

素因数分解をおこなっていって、$N = p^{2}q$で表せるような場合というのは、実は以下の二つのパターンしかないことに気づきます。

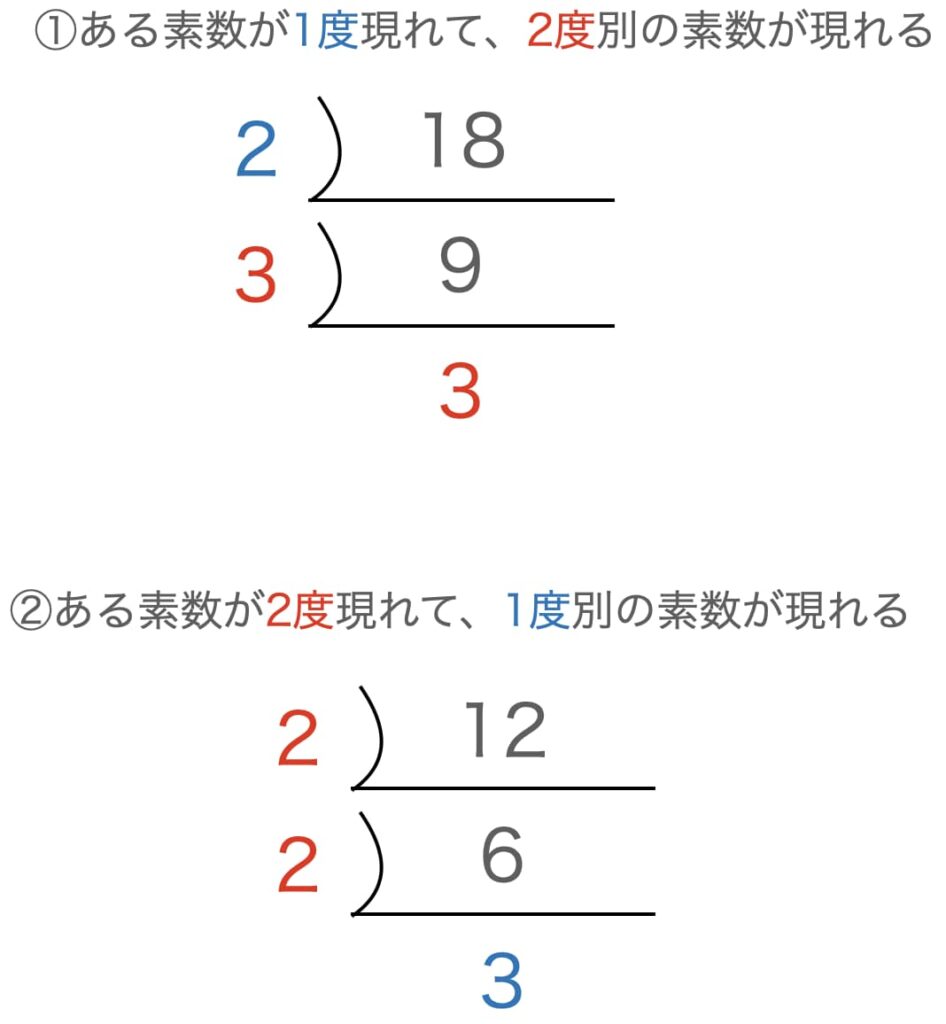
途中で掛け算することで $p^{2}q$ を作れる場合もあるんじゃないかと思う方もいるかもしれません。例えば以下のような感じですね。

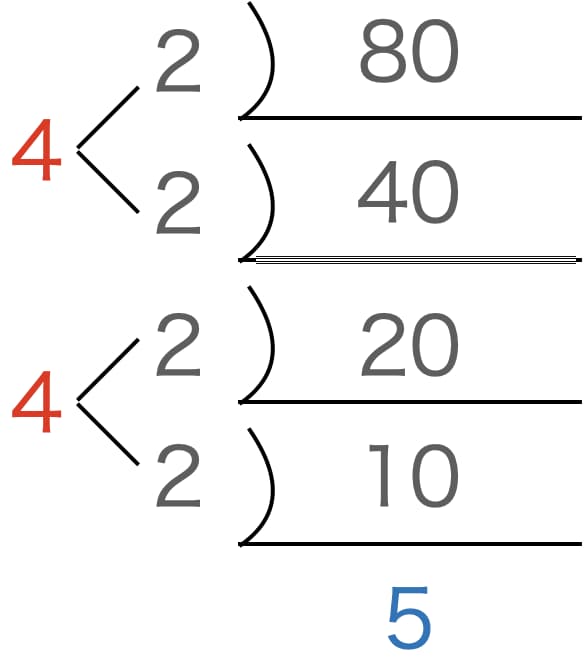
しかし、この場合は考えなくてもいいことはすぐにわかります。$2 \times 2$ をして作った 4 という数字は素数ではないからです。何かを掛け合わせて作った数字は少なくともその掛け算の要素で割り切ることができるので、素数の定義と矛盾します。

ここからわかるのは、試し割りをしていった際に少なくとも一方の素数だけがわかれば良いということです。

先ほどの例で考えてみましょう。2 という数字が分かった時点で後に続く数字のパターンは 2 通りしかないです。

①のケースに合致するなら 2 => 2 => （別の素数） と数字が続く

②のケースに合致するなら 2 =>（別の素数）=>（別の素数）と数字が続く

で、①、②のケースどっちに該当するのかは、N を現れた素数の 2 乗で割り切れるかどうかを試せば良いです。割り切れるなら①、割り切れないなら②のケースとなります。なぜなら割り切れないなら残りの素数は小数だ、ということになります。それは素数の定義と矛盾します。

①、②のケースのどちらかだとわかれば別の素数は計算で求めることができます。分かった数字を A とすると以下の通りですね。

①のケースの場合は、$p = A, q = N / A^{2}$

②のケースの場合は、$p = \sqrt{\frac{N}{A}}, q = A$

でもそれだと結局 $\sqrt{N}$ 回のループで試し割りをする必要があることに変わりはありません。しかしこのケースだと実は $\sqrt[3]{N}$ までの素数を見るだけで p, q の少なくともどちらか一方の小さい方の値が必ず分かります。

これは実際に $p^{2}q$ に代表的な値を入れてみると一目瞭然です。（代表的な値を入れてみるというのは私的にはよくやるテクニックです。数学的な知識がなくても定理を想像することができるので、いろんなところに応用してみてくださいね！）

① $p < q$ の場合

この場合は $p$ に最大として考えられる $\sqrt[3]{N}$ を与えると、$q$ は少なくとも $\sqrt[3]{N} + 1$ になります。この場合 $p^{2}q$ の値がどうなるかみてみると…

$$(\sqrt[3]{N}\sqrt[3]{N})\cdot(\sqrt[3]{N}\ + 1) \\ = \sqrt[3]{N}\sqrt[3]{N}\sqrt[3]{N} + \sqrt[3]{N}\sqrt[3]{N} \\ = N + (\sqrt[3]{N})^{2}$$

② $p > q$ の場合

こちらは $q$ に最大である $\sqrt[3]{N}$ を与えると $p$ は $\sqrt[3]{N} + 1$ が最も小さい値として考えられる値となります。この場合は、

$$(\sqrt[3]{N} + 1)^{2}\cdot\sqrt[3]{N} \\ = ((\sqrt[3]{N})^{2} + 2\sqrt[3]{N} + 1)\cdot\sqrt[3]{N} \\ = N + 2(\sqrt[3]{N})^{2} + \sqrt[3]{N}$$

どちらの場合でも明らかに N を超えてしまいます。ゆえに $p$, $q$ の少なくとも小さい方は $\sqrt[3]{N}$ より小さい値だということがわかります。

ここまで分かればあとはコードにするだけです。手順としては、

2 ~ $\sqrt[3]{N}$ のなかで N を割り切れる値を探す（この値を A とする）
割り切れる値が分かったら、N を A の 2 乗で割って割り切れるかを試す
- 割り切れる場合は、$p = A, q = N / A^{2}$ が答え
- 割り切れない場合は、$p = \sqrt{\frac{N}{A}}, q = A$ が答え

以下に回答として提出したコードを示します。

#include <bits/stdc++.h>
using namespace std;

int main() {
  int t;
  cin >> t;

  for (int i = 0; i < t; ++i) {
    long long N;
    cin >> N;

    long long A;
    for (long long j = 2; j * j * j <= N; ++j) {
      if (N % j == 0) {
        A = j;
        break;
      }
    }

    long long p, q;
    if (N % (A * A) == 0) {
      p = A;
      q = N / A / A;
    } else {
      p = sqrt(N / A);
      q = A;
    }

    cout << p << " " << q << endl;
  }

  return 0;
}